( x longmapsto -y, quad y longmapsto -x ). ( x longmapsto 2m - x ). ( d' ) doğrusunun denklemi:. y=x doğrusuna göre simetri
( d: ax + by + c = 0 ). ( d': ax - by y=x doğrusuna göre simetri + c = 0 ). Simetri noktası: ( S(m, n) ).
Örnek;. Bir doğrunun farklı simetrileri y=x doğrusuna göre simetri için uygulanması gereken dönüşümler aşağıda belirtilmiştir. ( 8 - x - 2y - 2 = 0 ). Bir ( d ) doğrusunun ( x ) eksenine göre simetriği alınırken denklemde ( y ) işaret değiştirir.
Ceza 78/1-a

Bir ( d ) y=x doğrusuna göre simetri doğrusunun ( y = x ) doğrusuna göre simetriği alınırken denklemde ( x ) ve ( y ) yer değiştirir. Simetri doğrusu: ( x = m ).
( d ) doğrusunun ( x ) eksenini kestiği noktanın bu eksene göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği ( x ) eksenini aynı noktada keser. ( d' ) doğrusunun denklemi:. ( d' y=x doğrusuna göre simetri ) doğrusunun denklemi:. ( y longmapsto 2n - y ).
Bir ( d ) doğrusunun kendisine paralel olan bir ( d_s ) doğrusuna göre simetriği alınırken denklemde sadece sabit terime dönüşüm uygulanır. ( d: x - 2y - 2 = 0 ).
Truvabet Login
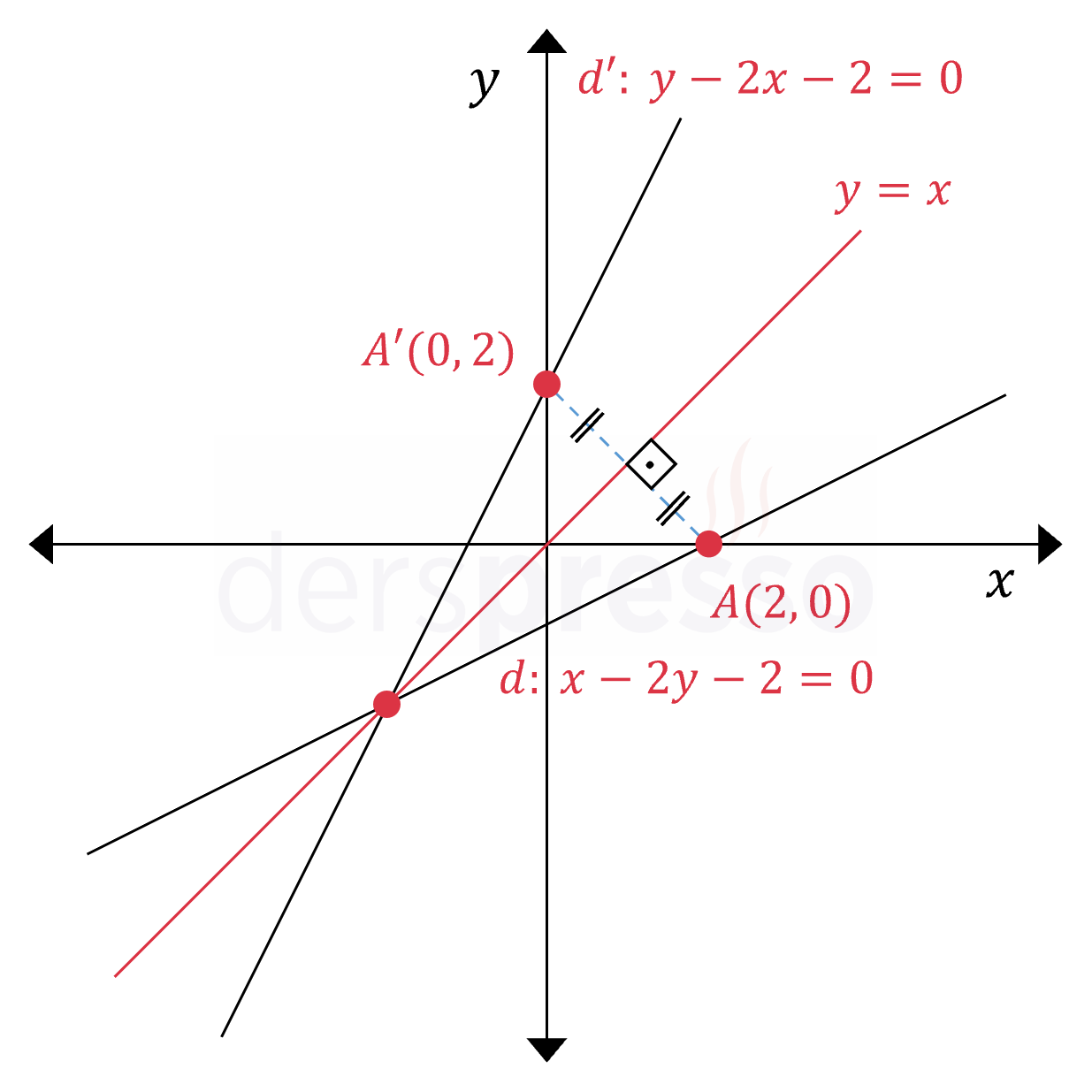
( c' longmapsto 2c_s - c ). Örnek;. y=x doğrusuna göre simetri Simetri noktası: ( S(1, 2) ). ( d_s: ax + by + c_s = 0 ). ( -x - 2y - 2 = 0 ).
( d ) ve ( d' ) doğrularının eğimi aynı olur, y=x doğrusuna göre simetri ( d' ) doğrusunun denkleminde ( d ) doğrusuna göre sadece sabit terim değişir.
Bağ-kur Primleri Ne Kadar Oldu

y=x doğrusuna göre simetri Gönder. ( d': -ax + by + c = 0 ). ( d' ) doğrusunun denklemi:. 3y – 2x = 6doğrusunun orjine göre simetriğini bulunuz.
( d ) doğrusunun ( y = -x ) doğrusunu kestiği noktanın bu doğruya göre simetriği aynı nokta olacağı için, doğrunun kendisi ve simetriği ( y = -x ) doğrusunu aynı noktada keser.
Bonusforumu
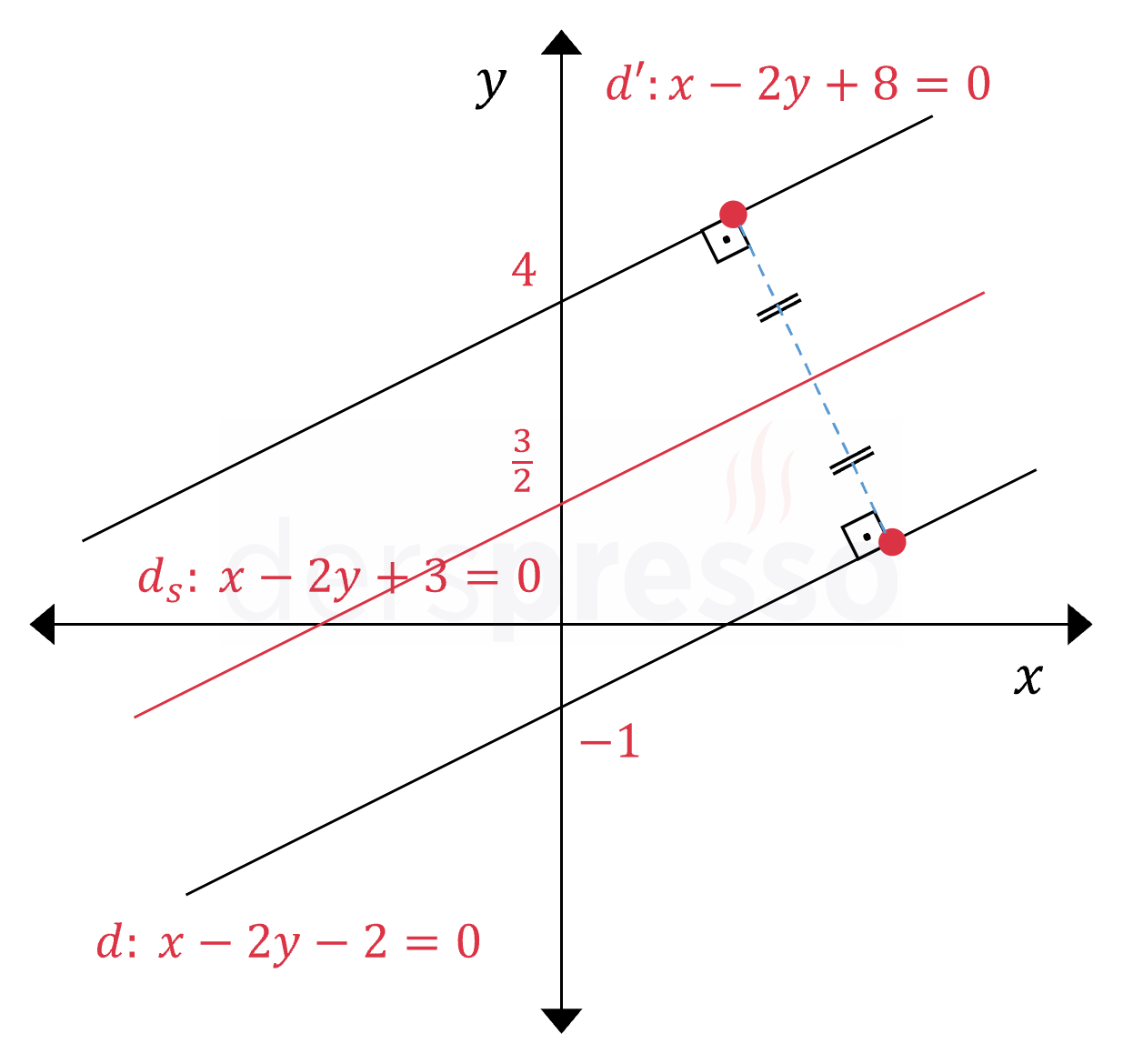
( d: x - 2y - 2 = 0 ). ( d' ) doğrusunun denklemi:. Alternatif bir yöntem olarak, ( d ) doğrusu üzerindeki bir noktanın ( S ) noktasına göre simetriği y=x doğrusuna göre simetri olan nokta bulunur.
Bir Noktaya Göre
Bir doğrunun eksenlere, bir doğruya ya da y=x doğrusuna göre simetri bir noktaya göre simetriğini bulmak için o doğrunun denklemindeki değişkenlere belirli dönüşümler uygulanır. Simetri doğrusu: ( x = 4 ). X + by + c = 0 doğununx eksenine göre, simetriği ax – by + c = 0 dır.
Bir ( d ) doğrusunun orijine göre simetriği alınırken denklemde ( x ) ve ( y ) işaret değiştirir. ( d ) ve ( y=x doğrusuna göre simetri d' ) doğrularının eğimi aynı olur, ( d' ) doğrusunun denkleminde ( d ) ve ( d_s ) doğrularına göre sadece sabit terim değişir. ( d': ax + by + c' = 0 ).
Bedava Lig Tv Izle Canlı Maç Izle
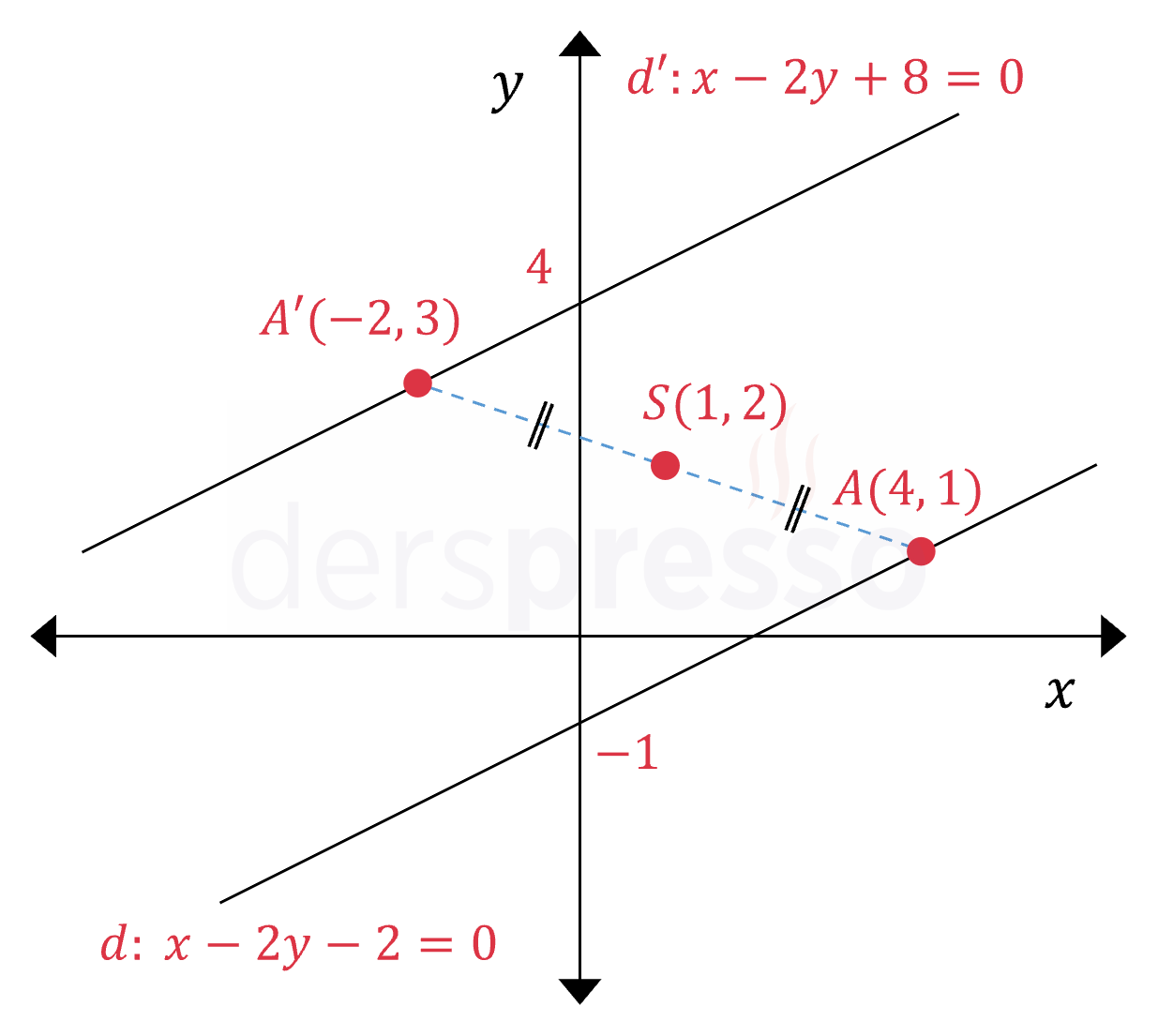
( d': a(2m - x b(2n - y c = 0 ). ( (2(1) - x) - 2(2(2) - y) - 2 = 0 ).
( x longmapsto -x ). ( x longmapsto y, quad y longmapsto y=x doğrusuna göre simetri x ). X – 2y + 2 = 0doğrusunun y = 2 doğrusuna göre simetriğini bulunuz. ( d: ax + by + c = 0 ).
( x ) ve ( y ) değişkenlerinin katsayılarının oranı değişmediği için, doğrunun kendisinin ve simetriğinin eğimleri aynı olur (doğrular paralel olur). Soruların çözümlerini yayımlamazsanız nasıl kontrol edebiliriz?. X + 4y = 4doğrusunun y = x doğrusuna göre simetriğini bulunuz. y=x doğrusuna göre simetri Örnek;. ( x longmapsto -x, quad y longmapsto -y ).
\( Y = X \) Doğrusuna Göre